Integer square root

This algorithm is a port of my PDP11 code from the 1970s. I had then only a vague understanding of why it worked. No less vague now. It has to do with the difference between squares being successive odd numbers?

It ported very nicely. On the '11 I used registers; on the C18 I use the stack. But the '11 had more shifts and compares.

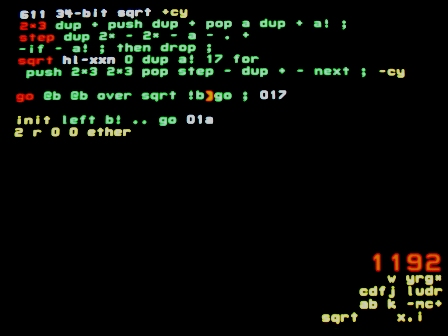
34 bit square root

2*3

• Add the low-order word to itself (shift left). It doesn't matter what the carry-in is. That only affects the low-order bit, which is never used. The code dup + does not require a . because there is no ripple to wait for
• Add the high-order word to itself
• Add register a to itself. a is a scratch register containing the high-order bits. It's initialized to 0
• Carry will be 0, since a must not overflow or the code fails

step

• Construct a trial divisor by shifting 01 into the stack
• If possible, subtract from a

sqrt

• 18 times:
  • Shift 3 words (stack and a) left 2 places
  • Call step
  • Shift the (inverted) carry bit into the stack

go