Gaussian function
This is the curve of the normal distribution: e-x2/2. It's tricky to calculate because numbers get so large (small) in the tail. This version works to maybe 4 sigma, before overflowing.

I use it to validate the normal distribution of random numbers. A display of this function is superimposed on them, and even grows along with them. It's a fun, dynamic display.
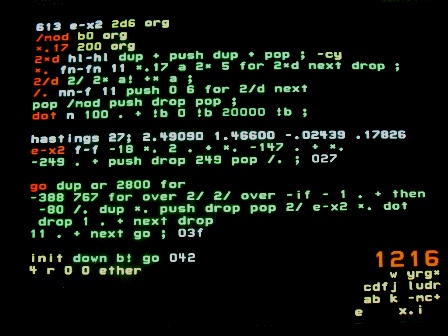
This code in block 1216 is loaded into node 613. It talks to node 713 which provides a run-length display in green.
Arithmetic
The arithmetic required for this calculation is educational. I'm using 11-bit fractions which require extra shifting.
*.
- The usual 17-bit signed-fraction multiply
- Register a is retrieved and shifted left (this is left-over from the left-shift in ROM)
- Now have the complete 36-bit product, with 11+11+1 fraction bits
- Shift it left 6 bits. This makes 29 fraction bits of which 11 (29-18) are now in the high-order word
/.
- We're dividing 2 numbers, integers or aligned fractions (dividend positive, divisor negative)
- Provide a 0 low-order word to make a 36-bit dividend. Think of it as adding 18 fraction bits
- Shift it right 7 bits, so 11 fraction bits remain
- Do a normal divide, discarding the remainder
- The quotient is an 18-bit fraction
Function
The approximation is from Hastings' Approximations for Digital Computers, Princeton University Press, 1955, Sheet 27. An oldy but goody reference.
The approximation is 1 divided by a cubic polynomial in x2. I don't care about normalizing the area, so I normalize the fraction to an 11-bit 1. With x=4, (x2)3 is a really large number, so I divide x2 by 2 to help (that screws up the standard-deviation). I only use 2 decimal digits in the coefficients for the same reason. A different application would justify more work.
e-x2
The cryptic name is intended to suggest the funtion.
- 11-bit fraction on stack; range 0-25.
- Compute negative polynomial (since it's a divisor), discard multiplicand
- Divide normalized to 1.
go
- An infinite loop, starting amplitude at 0
- 2801 frames (1 minute)
- 768 scan lines, start index at -388 (instead of -384, to match histogram)
- Divide amplitude by 4 to provide room to calibrate
- Make index positive
- Convert to fraction with 'standard-deviation' 80
- Compute x2/2, discarding multiplicand
- Call e-x2 and multiply by amplitude
- Call dot to display
- Increment index
- Increment amplitude by 11 to track growing histogram


