35-bit sine and cosine

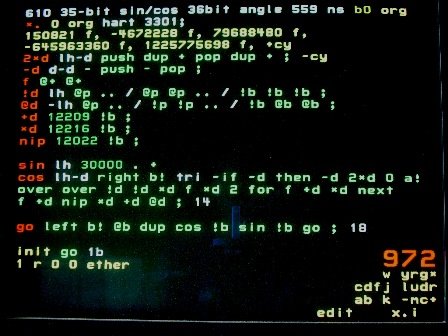
This code from block 972 is loaded into node 610. The input angle is an 36-bit fraction of a revolution; 1. is represented as 777777,777777. One bit is 40 micro-arcseconds. The cos is a 35-bit fraction, with 1. represented as 377777,777777. This provides 10-digit resolution.

*d +d

Double arithmetic is done be a neighbor node. It does a signed multiply or add of 35-bit fractions. A call to the proper routine is sent after the arguments. Fractions are stored on his stack. This is analogous to a floating-point coprocessor.

!d @d

Numbers are passed to/from the neighbor by instructions he'll execute from his comm port.

f

Fractions are fetched in order from an array at RAM address 0. They've been scaled to be 35-bit fractions and are sent to the neighbor by falling into !d.

sin

Sin is computed by subtracting 90^o from the high-order part of the input angle and falling into cos.

cos

The approximation used is taken from Computer Approximations by John F Hart, Wiley 1968; function 3301. This excellent reference has coefficients for many functions to various precisions. This approximation is

x(1 + a + bx² + cx⁴ + dx⁶ +ex⁸)

with a-e less than 1. Result is better than 8 digits between 0 and 90^o.

The input angle is an 36-bit fraction
The simple function tri (triangle) is computed as a linear approximation. It ramps up and down as does the cos and establishes the sign of the result. As the angle counts from 0-777777,777777
- tri starts at 377777,777777
- counts down by 2s to 000001,000000
- thence to -1, skipping 0
- counts down by 2s to 200000,000001 (largest negative number +1)
- repeats 200000,000001
- counts up by 2s to 377777,777777 (at angle 777777,777777)
- The repetition at the peaks will, of course, occur with the cos. This is how you want 35-bit fractions to behave
- The effect is that a half-bit has been added to the input angle
x is saved (over over) and squared
x² is multiplied by Hart's coefficients, scaled to 377777,777777
Which is then multiplied by x and x added

go

An infinite loop reading an angle from left (node 609) and returning sin and/or cos as desired.

Validation

I've compared cos with its 17-bit version and examined the 17-bit residual. I've displayed the residual of sin² + cos² - 1 which is a few bits from 0. And I've watched the bits near the peaks and zero crossings; all is as I expect.