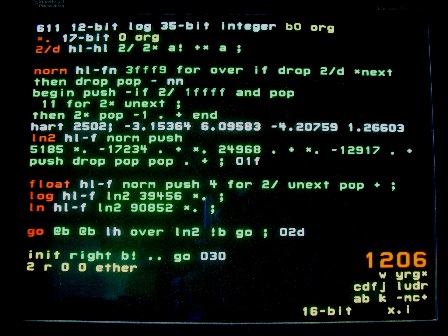
Logarithm
An interesting example of number representation. Uses a floating point number with a 12-bit mantissa and 6-bit exponent. Accurate to a couple of bits.
Checked for consistency with exponential. I'll tweak coefficients sometime.
The logarithm of a 35-bit integer uses this floating format. A positive exponent up to 17 is a left shift. A negative exponent up to -12 is a right shift.
Logarithm is useful for compressing a 35-bit number into an 18-bit number. And for doing logarithmic calculations (fractional powers). It's a standard library function, though I rarely need it.
*.
17-bit fraction multiply. Leaves multiplicand on stack
2/d
A 36-bit right shift that we've not used before. It does +* that will not add.
norm
Normalizes an integer producing a 12-bit fraction and 6-bit exponent.
- Shifts high-order right until it's 0. Counts shifts with next counter, offset to give right answer
- Shifts low-order left till it becomes negative. Decrements exponent
- Makes number a postive 17-bit fraction
- Shifts exponent into position

ln2
- Saves exponent
- Computes cubic polynomial of fraction. Coefficients from Hart, scaled to 12 bits
- Discards multiplicand
- Adds exponent
float
Combines mantissa and exponent to form a floating-point number. Just an example, it's not used.
log
Logarithm to base 10 is simple scaling.
ln
As is natural logarithm to base e.

