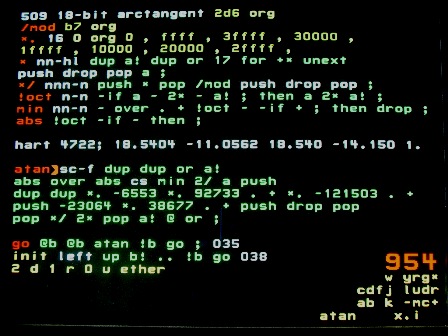
ArcTangent

Another interesting calculation:

It must reconcile the proper quadrant of the circle. A nice way of doing this is to require 2 arguments: sin and cos. Their signs determine the quadrant.
Which is the smaller determines the octant (45^o).
Hart has an approximation for arcsine between 0 and 45^o which is simpler than computing arctangent.
Finally, an offset for the original octant is added

Arithmetic

*/

This is a perfect application for */. A number is multiplied by a ratio. I see it as simpler, faster and more accurate than /. and *..

!oct

Shifts a sign bit into register a. Uses the trick - 2* - to shift in a 1.

min

The standard library function is modified by adding a call to !oct at the right time.

abs

The standard library function is modified by adding a call to !oct.

Function

Hart's approximation is:

arcsin(x) = x(a + bx²)/(c + dx² + ex⁴)

It's good to 5 decimals. His coefficients compute the angle in radians. I scale the numerator to produce the right answer at sin(45^o). This requires multiplying by 65536/10pi to get a 16-bit fraction. The denominator is multiplied by 65536/10.

A table of offsets for the 8 octants is stored at 0. When the computed 15-bit angle is added, the result will be an 18-bit fraction. Half the octants require the angle be reversed.

atan

Arguments are 2 17-bit fractions, cos on top, sin beneath.

(atan will leave stuff on the stack. Doesn't matter since it's so big it will always have its own node.)

The octant is coded as the number csr

c is the sign of cos
s is the sign of sin
r is 1 if cos is smaller than sin

So the order of the octant table in normal octant numbering is: 0, 1, 7, 6, 3, 2, 4, 5.

The octant is built in register a. First the sign of the cos, then the sign of the sin, then their comparison
After the smaller positive fraction is chosen, it's divided by 2 into a 16-bit fraction and squared
The negative denominator is calculated
Then the numerator
Then a 15-bit angle
Which is augmented from the octant table. An or is used (instead of +). That seems to tweak the bits just right

Validation

Given an angle, sin and cos are computed and from them atan. The result is compared to the original angle.

I can display 768 points at a time and have done so for various samplings of the 262,144 possible angles. Error seems to be +- 1 bit. Further testing will be done when atan is used.