3-d vector arithmetic
It's expected that vectors are 16-bit fractions.
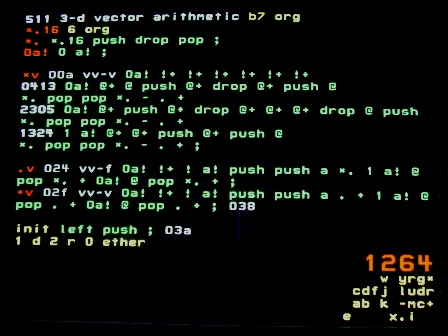
Storage
Space is left at address 0 to store two 3-vectors. This seems optimal for their cross-product.
*.
16-bit fraction multiply, discarding multiplicand
*v
Cross product. Wikipedia lists the result as
- Given b3 b2 b1 a3 a2 a1 on the stack
- Return a1b2-a2b1 a3b1-a1b3 a2b3-a3b2
- This requires random access to components
A neat way of access is to save all components. Then read through them, saving those needed on stack and return stack
- Save vectors
- For the 3rd component, read 5 components: save 0 and 4 on the stack; 1 and 3 on the return stack
- Multiply the stack
- Multiply the return stack and subtract
- Similarly for the other 2 components
.v
Dot product.
- Use storage at 0 for 2 components of first vector, a for 3rd
- Push 2 components of second vector
- Multiply 3rd components
- Multiply and add 2nd and 1st components
+v
Add 2 vectors. Similar storage as for .v.